1D: Variable Acceleration
No idea what to think. Got no experience with calculus based questions.

58 Replies
@Gyro Gearloose
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.$$ma = -mg + -mkv$$
$$a = -g +{-k}v$$
$$ \frac{dv}{g+kv} = -dt$$
$$\int{20}^{v} \frac{dv}{g+kv} = \int{0}^{t}dt$$
$$\frac{1}{k} log(g+kv) = -t$$
applying limits and solving we get
$$ v = 20 e^{-kt} + \frac{g}{k} (e^{-kt} -1)$$
Energy conservation?
there's an external force
+ non-conservative
You have taken upward direction positive?
that negative in the given expression shows that its always opposite of velocity
Yeah same thing
Keshav
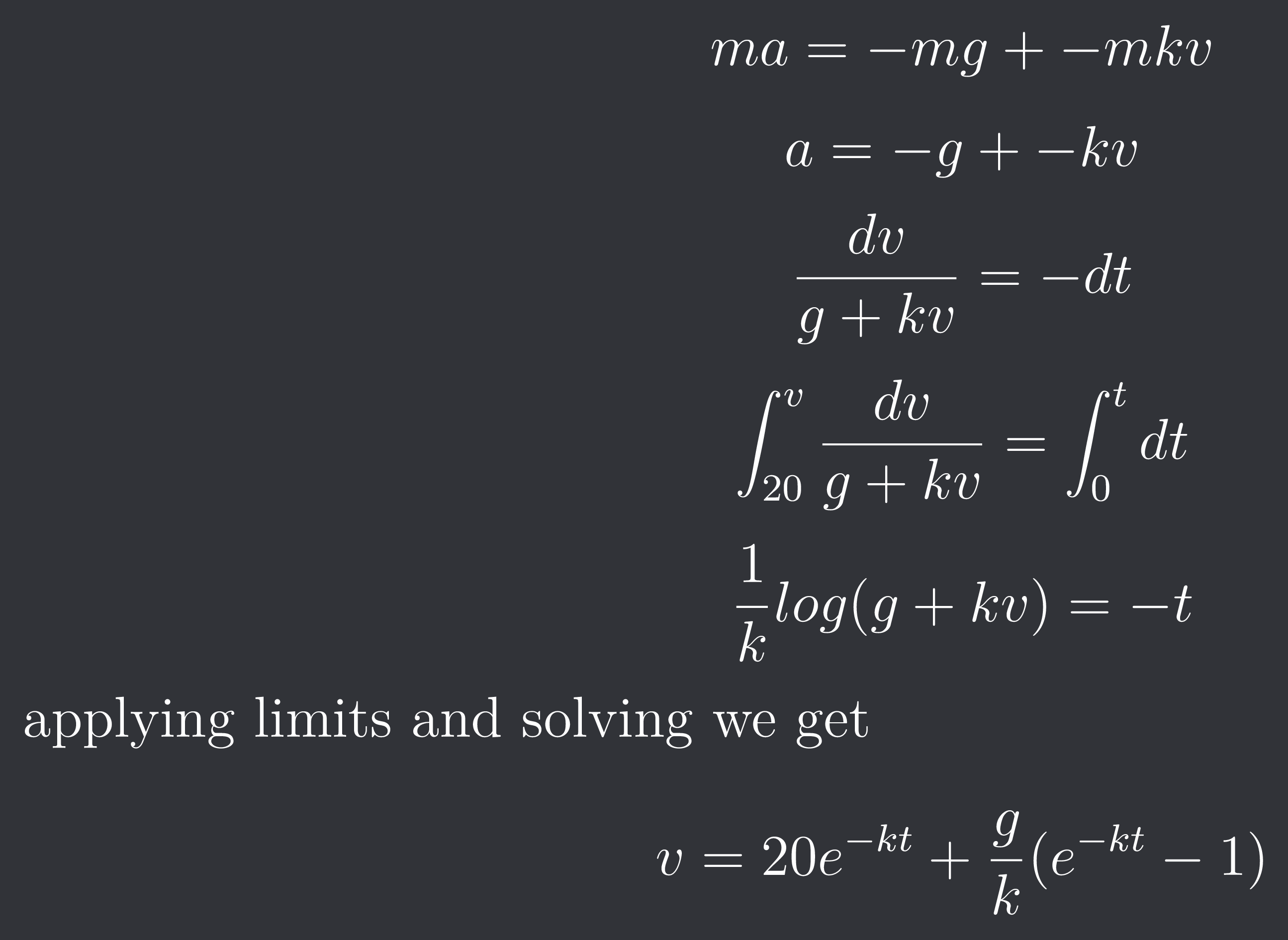
this qs is from kevin zhou's handout

How did you write the 3rd step?
Is it a famous book?
$$\frac{dv}{dt} = -(g +{k}v)$$
$$ \frac{dv}{g+kv} = -dt$$
Keshav
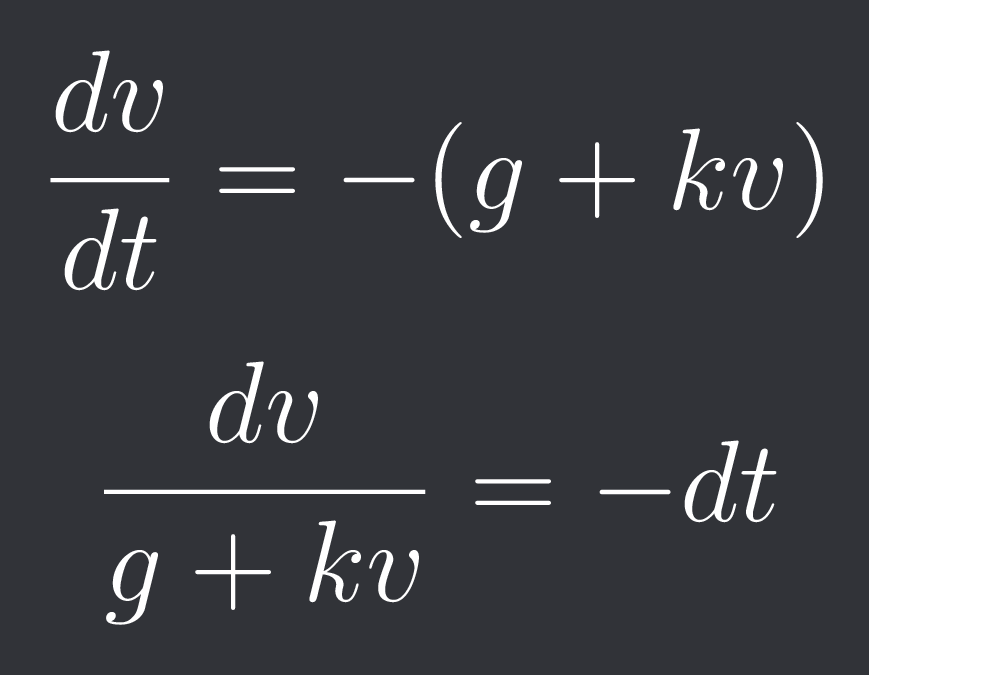
Got it
a famous one for Physics Olympiad, yeah
its a handout
by multiplying both sides by dt
Yeah sorry didn't see that
now try solving the same qs for $a_{drag} = -\alpha v^2$
So then you applied the limits to integrate
Keshav

yeah
integrate and then apply limits
What's the max height?
taking g = 10, k = 2
we can write
$$\frac{dx}{dt} = 25 e^{-kt} + 5 $$
Keshav
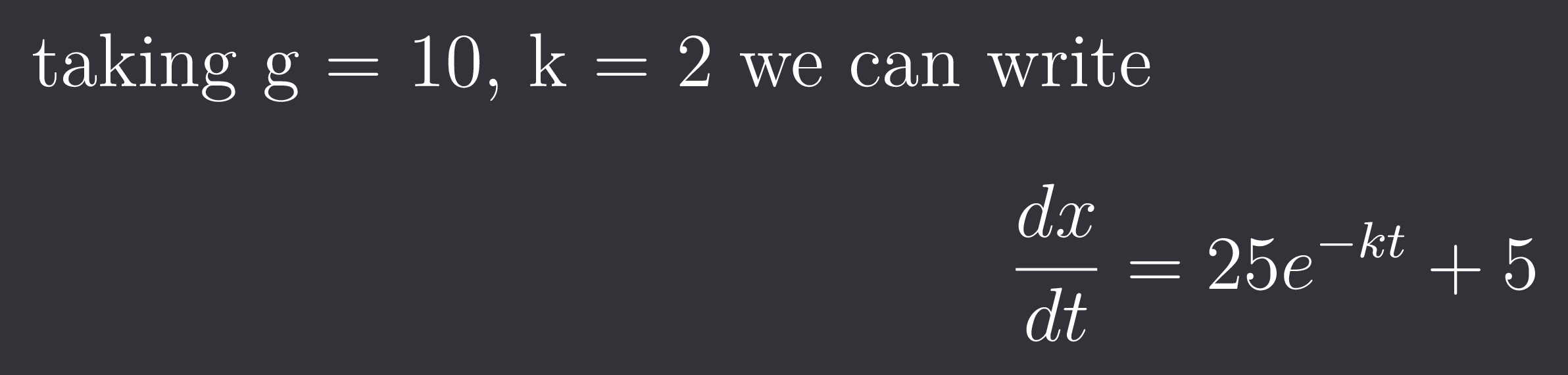
now at max height
dx/dt = 0
How did you integrate that in the 4th step?
$$\int \frac{dv}{g+kv} $$
$$u= g+kv$$
$$du = kdv$$
$$\frac{1}{k} \int \frac{du}{u} $$
$$\frac{1}{k} ln(u)$$
$$\frac{1}{k} ln(g+kv)$$
Keshav
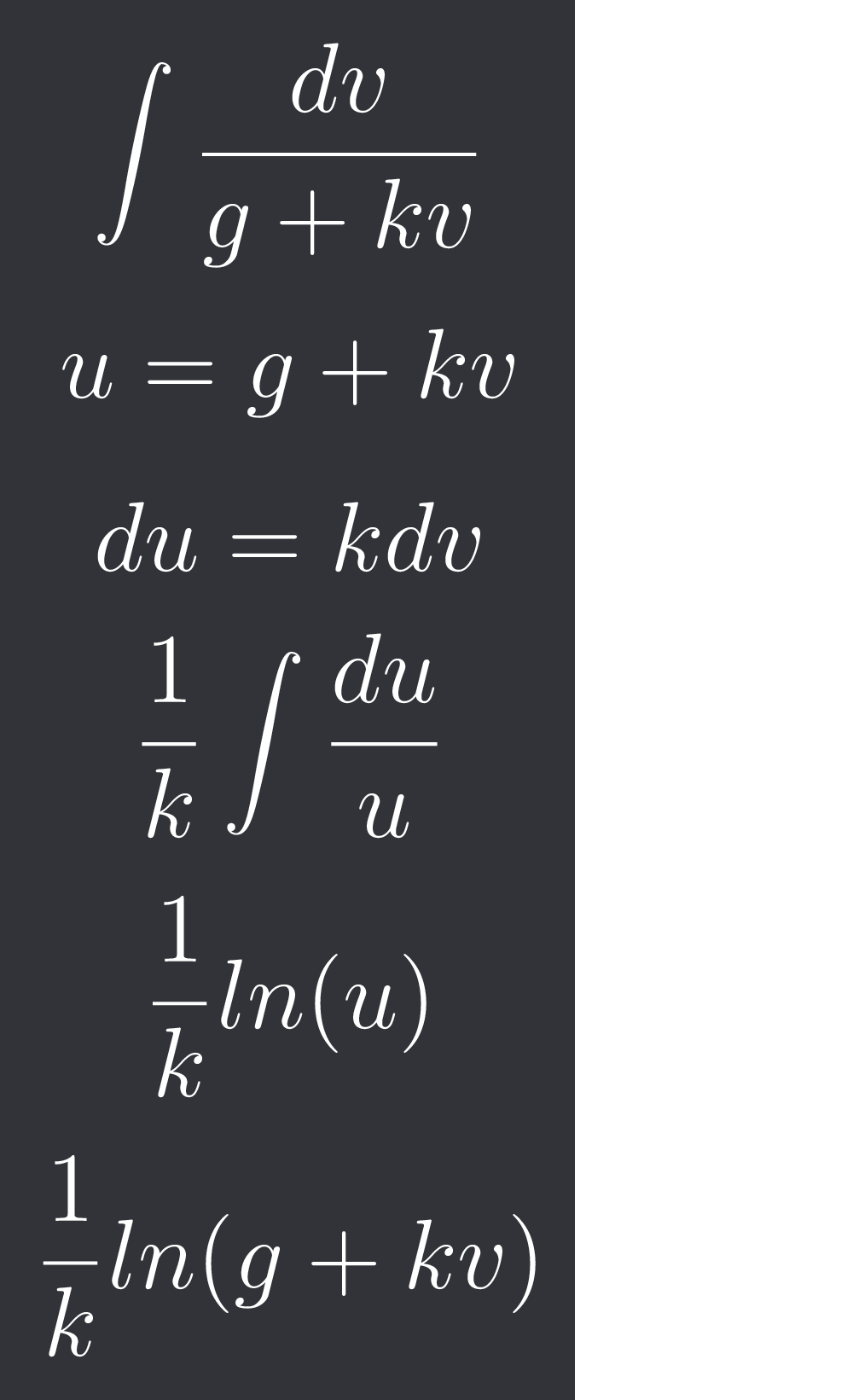
u is combined accn?
no, we integrate stuff by substitution
search yt for u-sub integral method
I'll be back after I learn this method
for ascent
net -ve acceleration= g+ kv/m
a= dv/dt, put this in eqn 1 (differential equation banega)and integrate, you'll get velocity wrt time
Got it

1/K is a constant right?
Stuck on the limits part. I got the expression.
Won't net -ve accn be (-g) + (-kv)?
Where am I wrong?
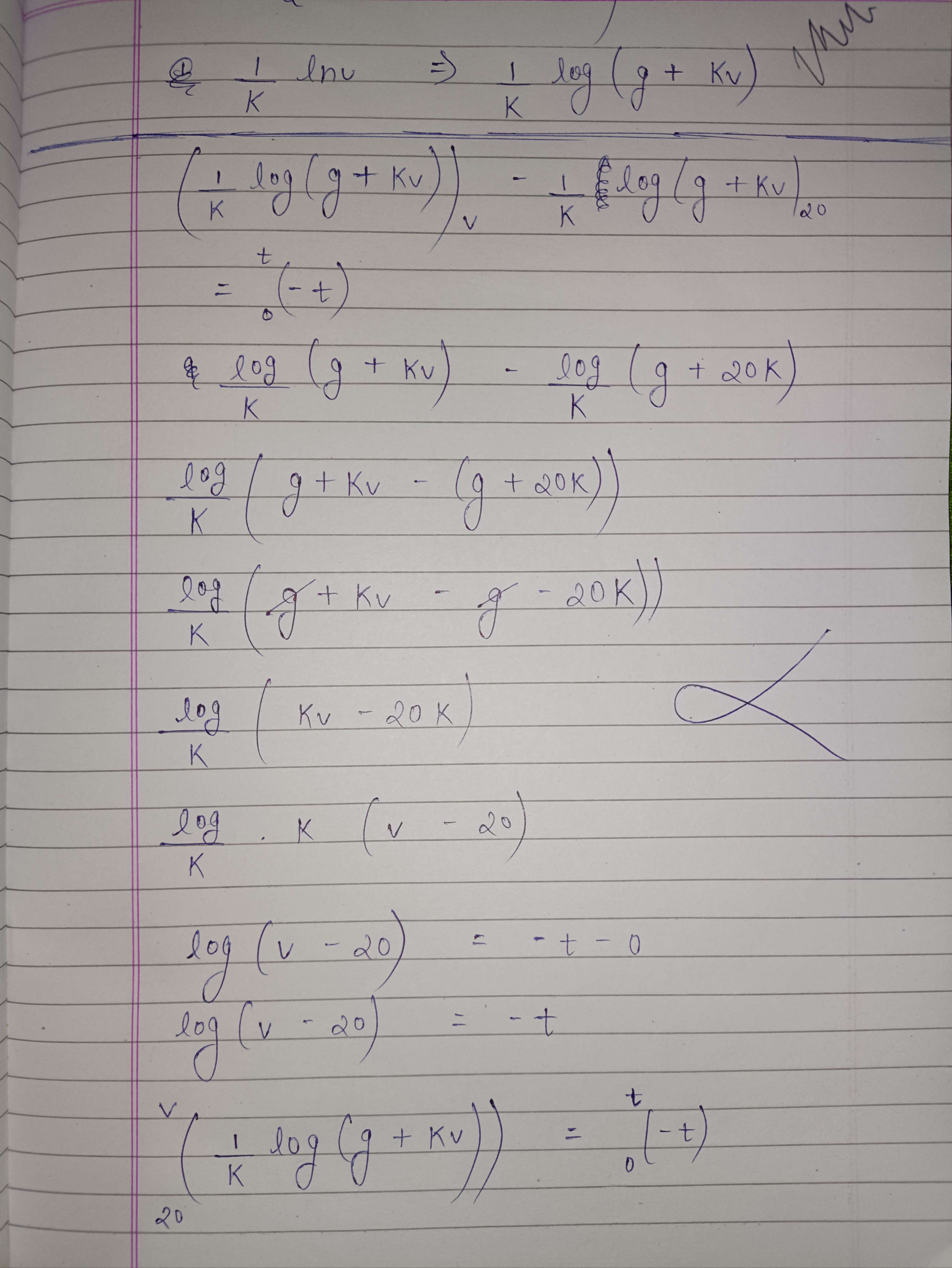
Wouldn't it be simpler to integrate as a function of x rather than t for the height?
i meant to say deceleration cus speed decreases while in ascent right
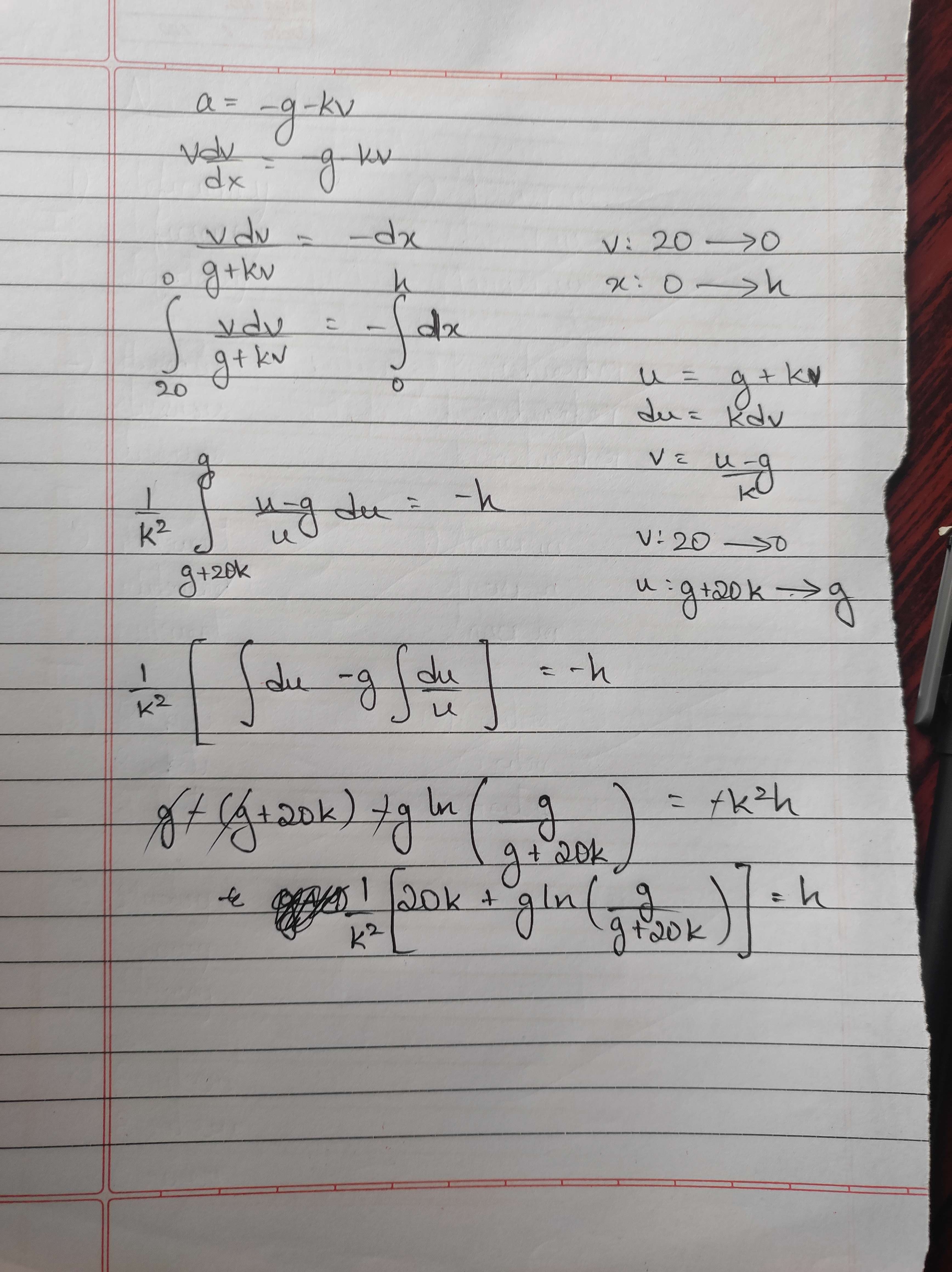
To calculate h. This is what I did.
It's gonna be as @Keshav did for the time of ascent
Uh
Yeah same thing
Is that sarcastic?
It's tough to tell with text messages.
Nope
I isolated dv to get du/k
Yeah I've done that.
I got Keshav's result
I took the 1/k outside the integral immediately.
I'm stuck on the limits part
My failed attempt

Time of descent is turning out to be a problem
Because we don't know final velocity when the body comes back down
Our teacher will explain to us this problem today
I got a transcendental equation in terms of time of descent

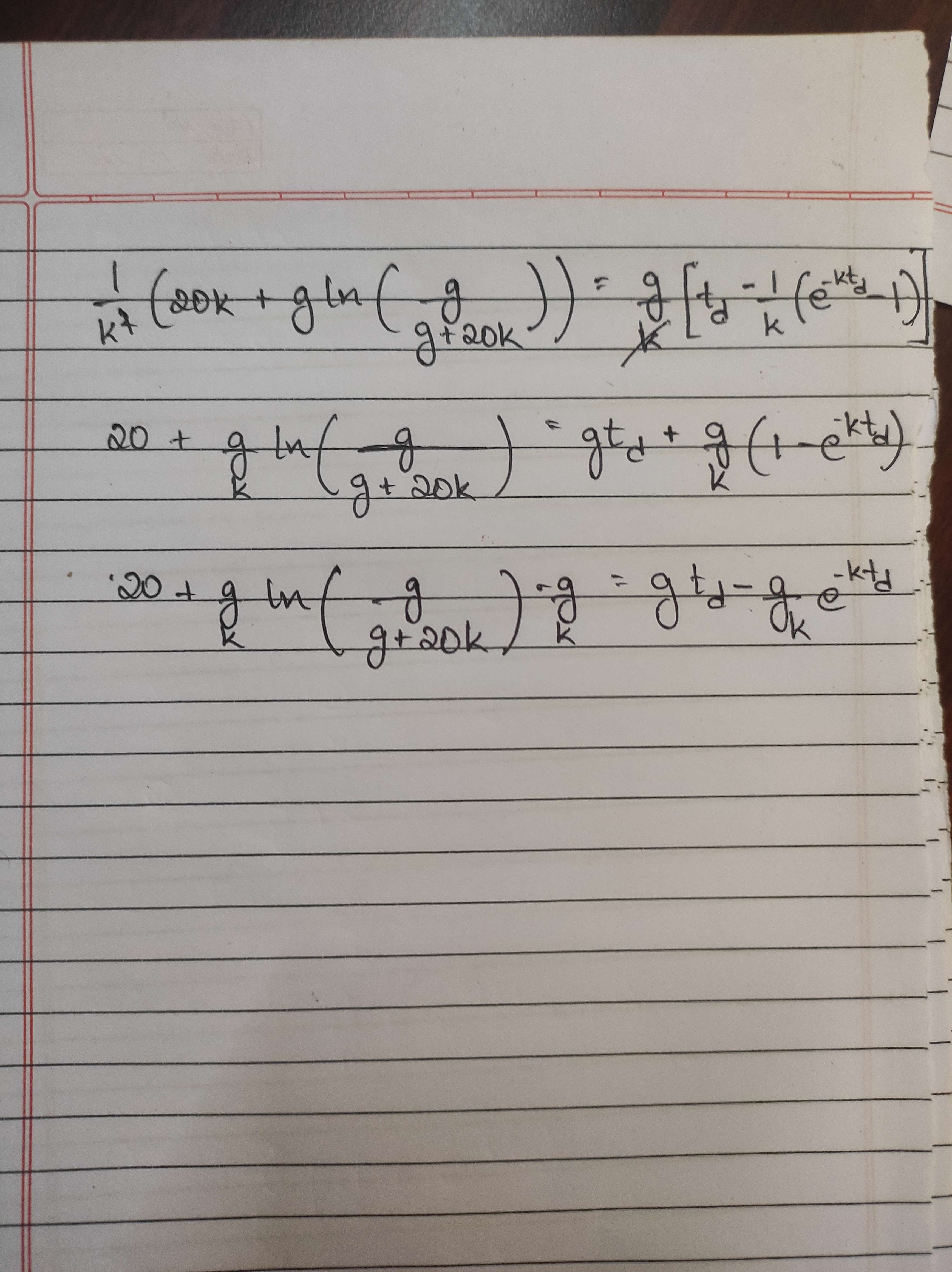
Yea I give up
That level of integration is out of my reach for now
The concept used in this question is simple, but it's made tough using the math
Just read calculus for the practical man and move on with Physics
Keshav, could you verify my solution for maximum height?
This one.
Good idea
got the time of ascent
for max height can we just do a=vdv/dx
plus in values and limits and integrate
got stuck at 3 and 4
+solved @Keshav
Post locked and archived successfully!
Archived by
<@624803801173327923> (624803801173327923)
Time
<t:1717264138:R>
Solved by
<@1082354613749035099> (1082354613749035099)