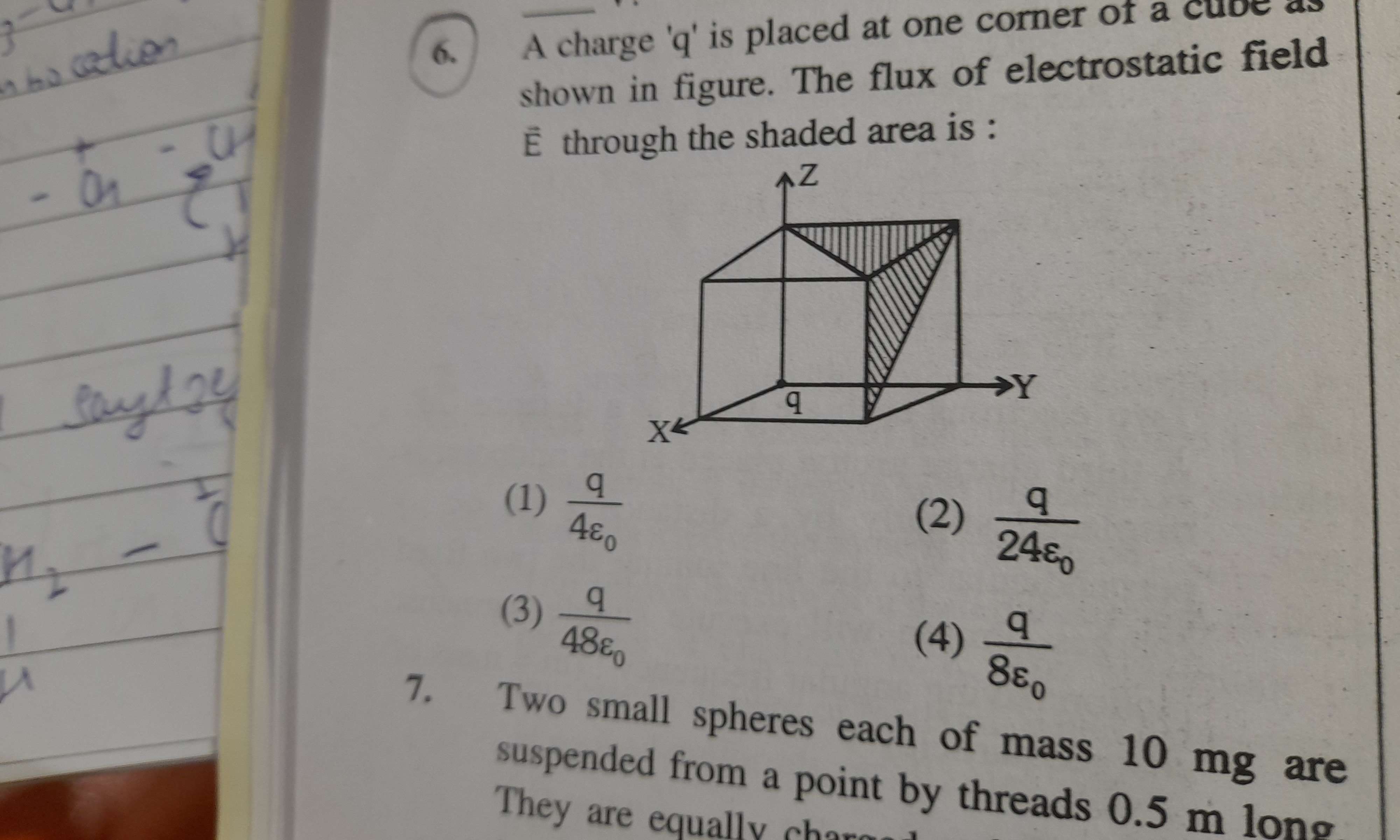
electrostat pyq
so in this q the answer is 2nd option but my doubt is that the 'q' charge isnt symmetrical with both points like it should be at equal distance and then only we can say that the shaded region is half shaded so two halves make one face and then we can go about the calc but since the point isnt symmetrical from the charge we cant say that its equal because the flux will be different right?
36 Replies
@Dexter
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.whoops sorry for the wrong ping-
Ok, this is a pretty standard practice question. So what you need to do is extend your Gaussian surface. Think of duplicating the cube seven more times so that you make a scaled up version of this cube such that the charge is now at the centre of the scaled up cube.
Actually, wait a couple mins. I'll draw it out and send a pic
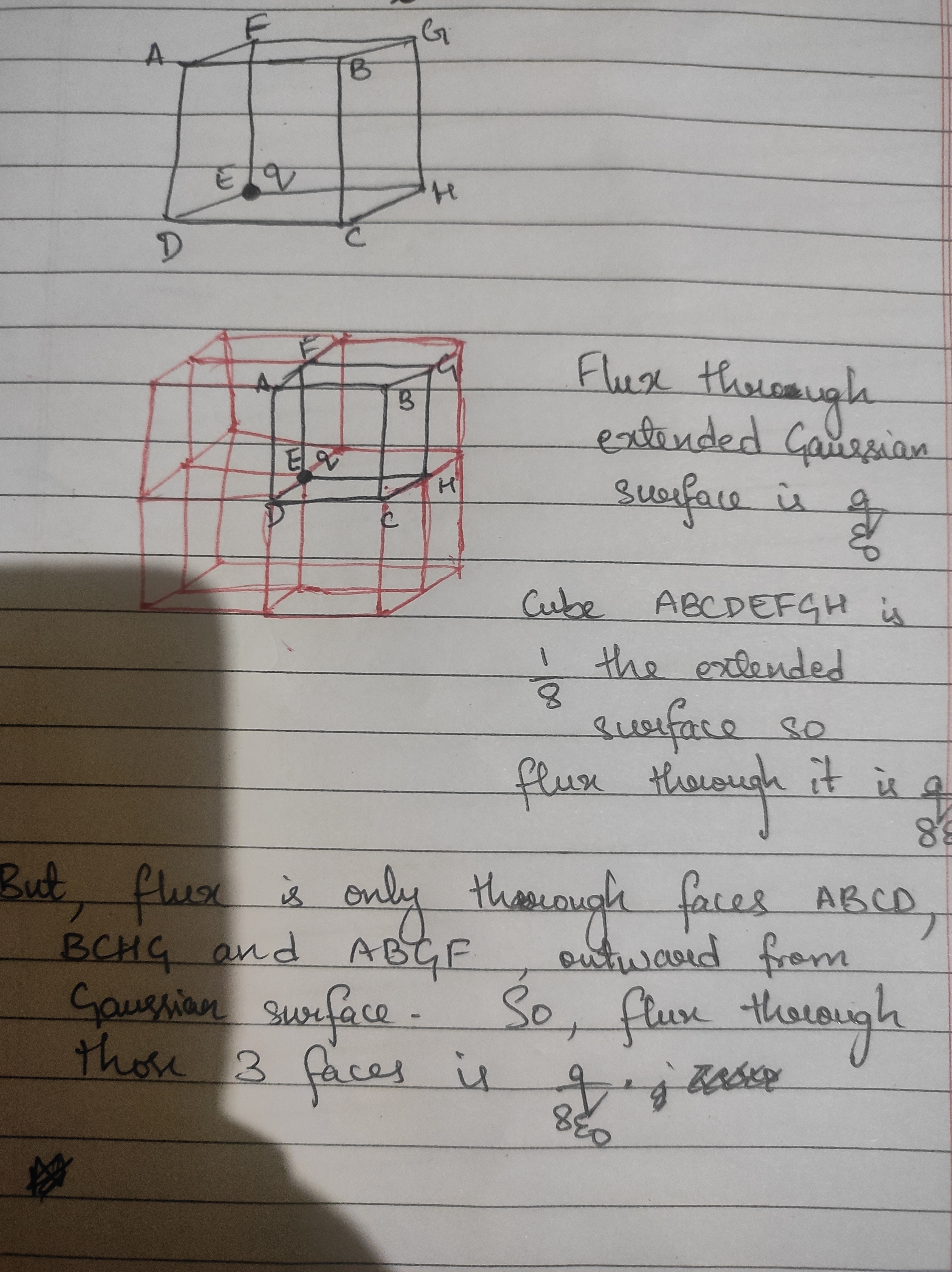
In the question, the total shaded area is 1 face which is 1/3 of the surface through which flux exists. So,( 1/3)(q/8ε) = q/24ε
@trin
lol pls read what i said
my doubt is that the flux at both the shaded regions cant be same because the position of q charge isnt at the same position from both the shaded regions so the electric field lines will be more thru some region and less thru the other one and hence we cant take it as "1" face
The flux through each might not be same but the sum is still one third of the total.
how can you say so
the answer which you've given is correct but i feel that the q has some gaps
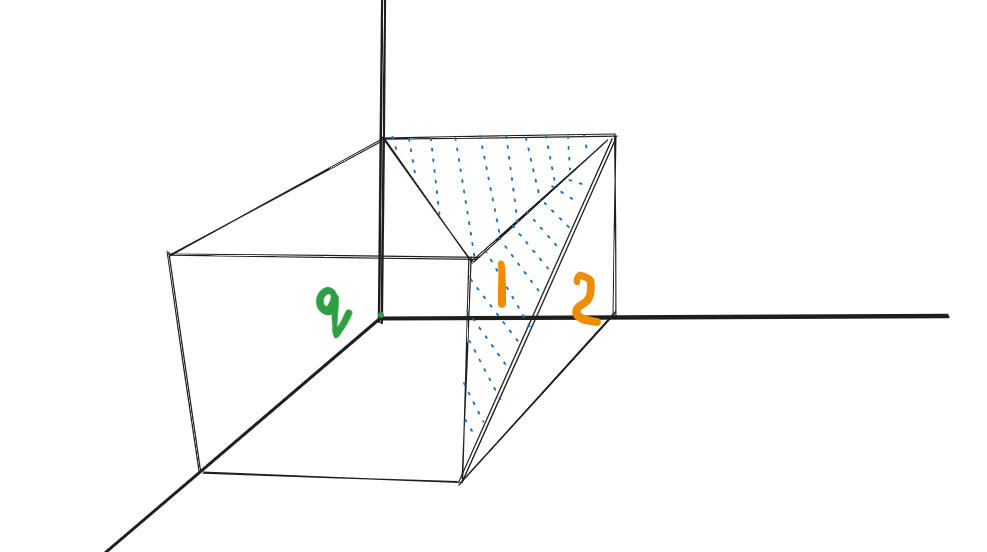
lemme ask my q thru an image
Wait. This is probably gonna mess my brain up but I'll just try a surface integral over the surface and check if it comes out to be the same.
okay!
...the parameters are messed up
so yeah over here the surface 1 and 2 are at different positions from the charge q so the flux should be different
Ye gods above. Why am I doing this? Look at the surface integral for just the first triangular part.
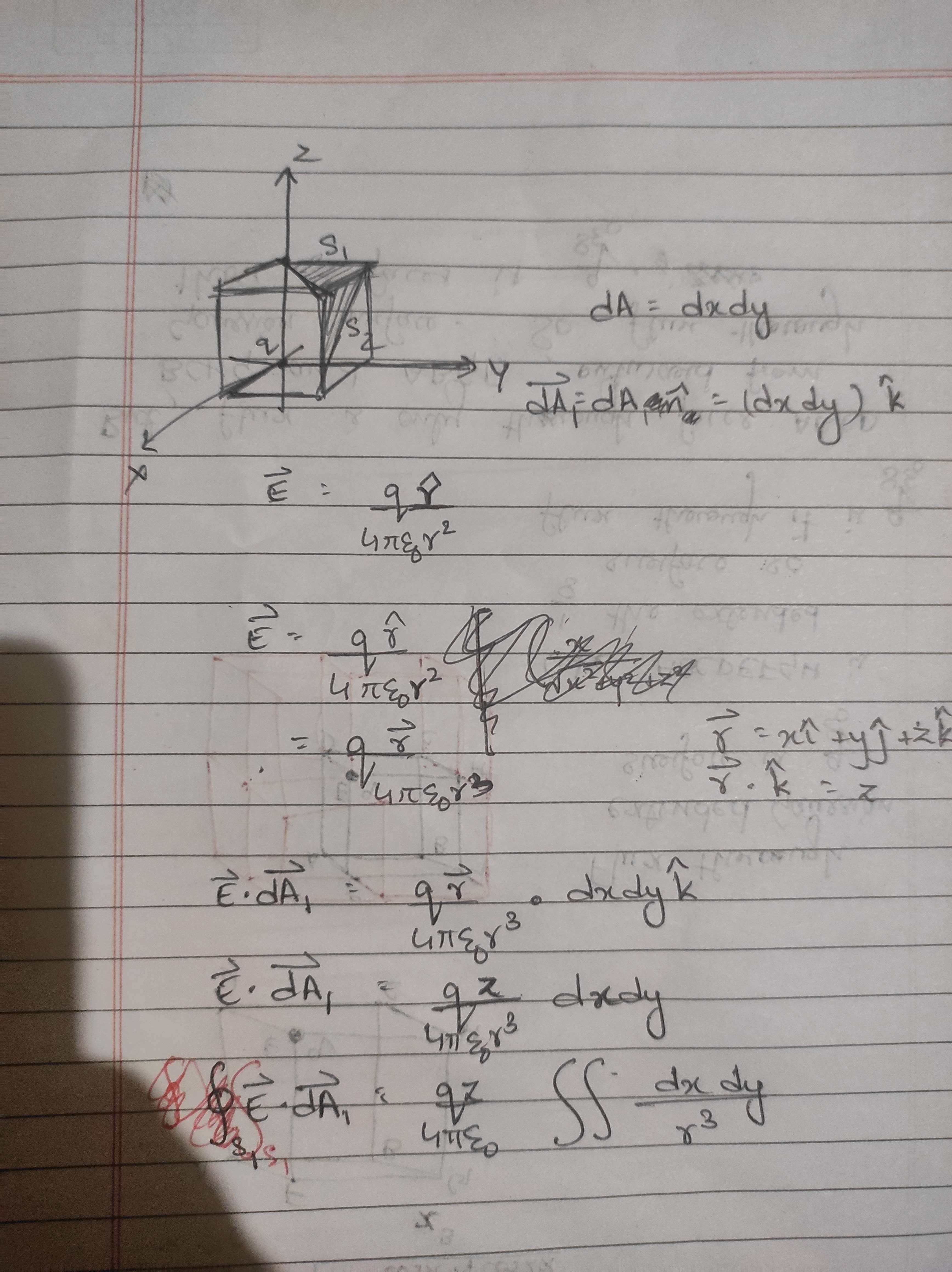
i mean you dont rlly need to do surface integral, its pretty obv that they arent same
whooopps
Tip no.one for physics.
Nothing is "pretty obvious".
😭
Okay wait. They are symmetrical
I'm dumb. Symmetric on rotation about the line passing through the origin(q) and the opposite vertex.
wdym?
The line x=y=z
Think of it as your axis of rotation. The surfaces are symmetrical on rotation. One vertex along an edge, one vertex across a face diagonal, and the opposite vertex. Symmetric on rotation.
but technically if we rotate it then the other surface would also rotate
Eh, we don't care about that anymore. We have determined the flux through the three other surfaces and that the required segments are symmetrical. Put those two facts together.
It's not the most rigorous process, but if we sat and tried to rigorously prove everything, we'd be pure maths students. I love me a rigorous proof but this is not the question for it.
can anyone else share their thoughts on this?
This question?

Ek cube ka q/8e flux nikalta h to isme 3 gaussian cube banne pdenge charge ko enclose krne k liye and then q/24 aajayega but fir tujhe isko 1/2 x 2 se multiply krna hoga kyuki flux 1/2 1/2 shaded face se pucha hai
They don't want the method. They want the proof.
Proof of what?
Of why the flux though the two half-faces is 1/3 of the flux through the 3 faces. As to where the symmetry lies.
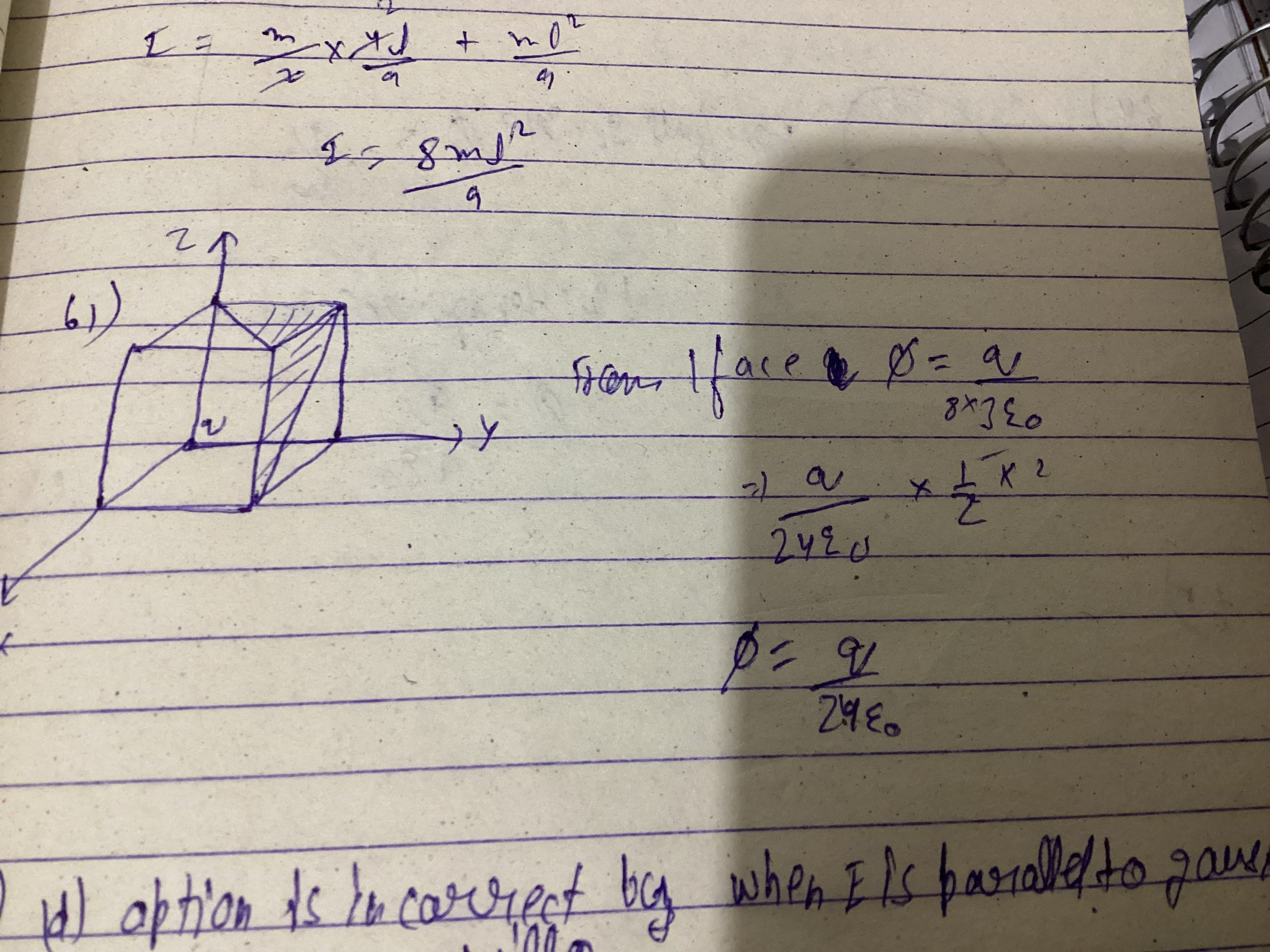
Ik lol. It's not me who asked the question
You mean why idivided 1/3?
I know. It's @trin who's asking
Ok 😅
hmm
nvm ill just let this slide
+solved @Opt
Post locked and archived successfully!
Archived by
<@852788017243357194> (852788017243357194)
Time
<t:1717214924:R>
Solved by
<@763645886500175892> (763645886500175892)