Trigno Limits
tex, limit x tends to 0
\frac{1-\cos\left(x\right)\sqrt{\cos\left(2x\right)}}{x^{2}}
30 Replies
@Apu
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.,tex $\lim_{x\to 0} \frac{1-\cos\left(x\right)\sqrt{\cos\left(2x\right)}}{x^{2}}
yo sup. nice formatting 🙂 is this q not happening? What did you try so far?
lhopital
i tried applying the standard 1-cosx/x^2 limit
can you please explain
u havent studied lhopital's rule?
i don't think so
well then w8
Ansh Agarwal
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
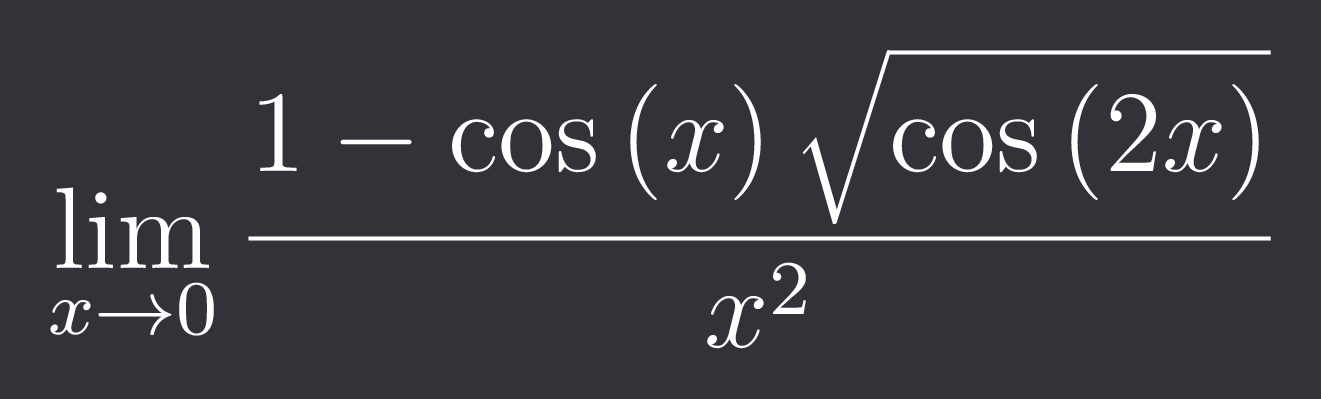
is it 0?
@Ansh Agarwal
3/2
T_T how men
idk , mera bhi 0 aa rha tha , then 1/2
(1- cos x) / x obv 0 ko tend karta hai
w8 lemme try lhopital
it would be a 0/0 form indeterminate
after trig manipulation it tends to 0
w8 mai lhopital se karke check karta , lemme eat dinner first
ok , thanks
+solved @Ansh Agarwal
Uh i remember doing this.
LDNE
The limit doesn't exist.
Nvm
It was similar but different. I'm dumb. That one was with sine, not cosine. This is just 3/2
3/2 kahan diya hai answer? Soln mein?
lim x->0 (1-cos x )/ x^2 = 1/2. Isse use karke jo root mein bachega usmein limit value put kardo.
Ans phir 1/2 mujhe aa rha hai.
L Hospital rule laga ke bahut hi jyada lamba ho jayega.
Im confused ki hows the ans 3/2. As far as im solving, im doing it right...
Did you rationalize the funtion then solve it to get 3/2?
Yup
Double L hopital did the trick
Yeahh it will, but that is very lenghty. You can rationalize the funtion and solve as well
my doubt is, what is wrong with the method in which im getting ans as 1/2?
One of mates solved it via Taylor series
(Ig he was the only one who did it via l hopital)
Ye yaha nahi lag payaga coz of the 2nd cos
Even if you break it into 2 this won't work
Why? I mean I know breaking it into 2 is the reason its not working, but why cant i break it into 2?
For that you need to see how the rule was made
The rule made using series expansion (the proof of which is college level maths)
Which does not allow for it being broken like this
The taylor series expansion?
I am not sure about that tbh
Coool no worries, thanks tho!
+solved @KaiZên
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1718990524:R>
Solved by
<@759468963884564502> (759468963884564502)