21 Replies
@Apu
@Apu
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.sorry pinged twice
🤔 damn I'll check
Hey! Did you click on the button once or twice?
hey have you tried smth by IBP?
twice if i remember correctly
yeah, it was getting really lengthy. i did it like 2-3 times but im hitting dead ends
.
Comrade Rock Astley
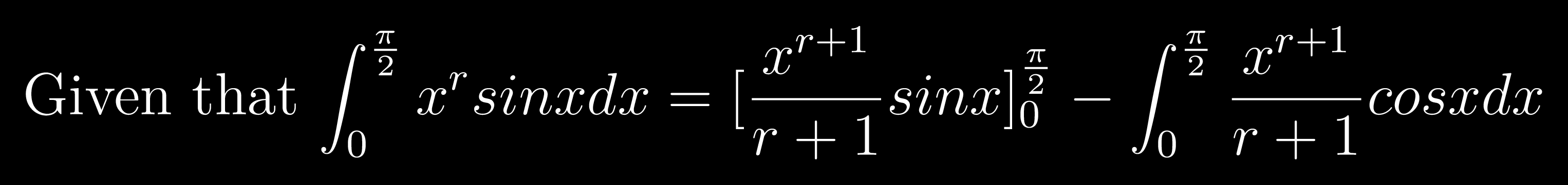
Since the denominator is a definite integral let it be some k
one sec I'll work on it
Well
there's a not so complicated method
Expand sinx and cosx using Taylor series expansions
You get this
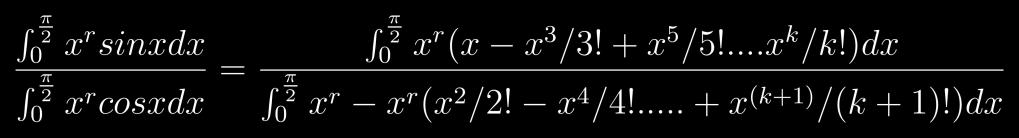
Here k is some infinitely large number
You can now drop all terms except the one with the largest exponent
This gives you
Comrade Rock Astley
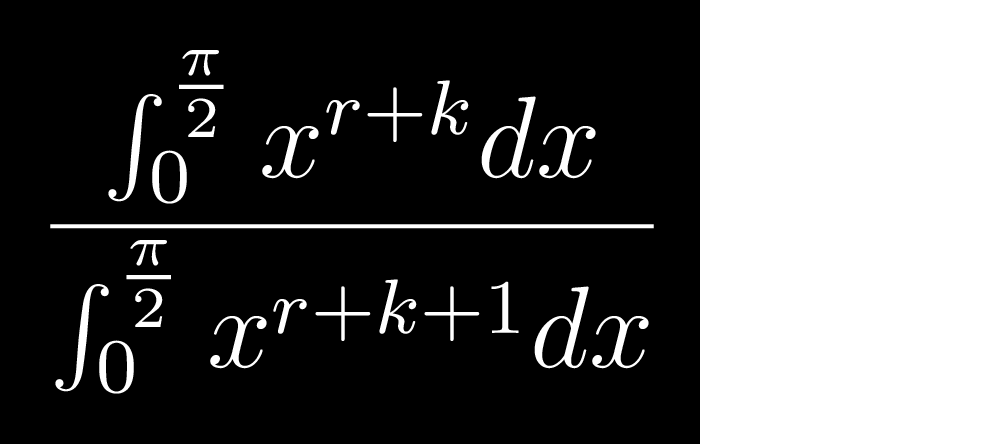
Now we can cancel the denominators after integration since they're practically equal
So this reduces to 2/pi
Comrade Rock Astley
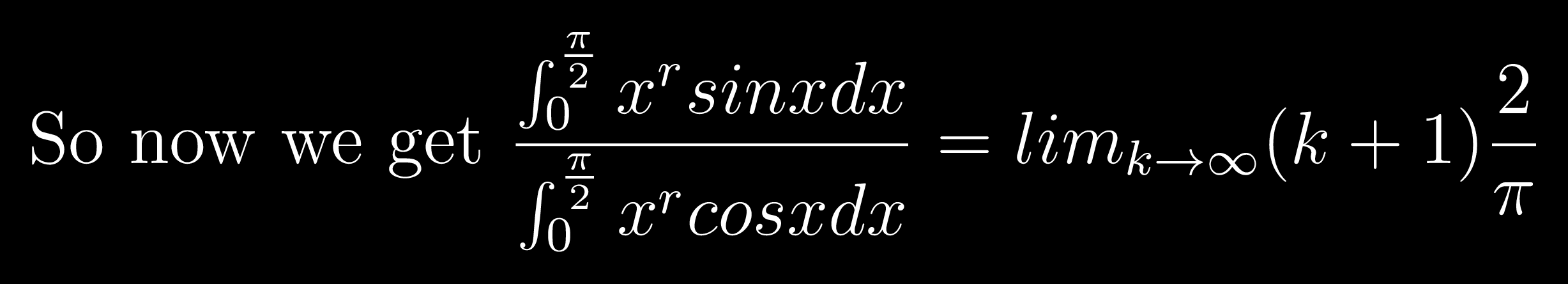
so
C=-1
so that r and k cancel out
L = 2/pi
answer is 3
now there's one thing left to explain...the reason I've used k+1 instead of k-1 or any other number in the denominator is so that we get the result, but...there's gotta be a logical reason for that
We know sin^2x + cos^2x=1 for all x. Hence we note that sin^2x+cos^2x does not depend on x. Now the highest exponent in the terms of sin^2x here is x^2k. To cancel it we’ll need the terms in cos^2x formed by the multiplying x^k-1 and x^k+1
If x^k-1 is the largest term in cosx, it can be proven that there is always a positive term of x^2k in the expression sin^2x+cos^2x that won’t cancel out
It won’t cancel out perfectly, but when all other terms are included they cancel out in the end
and that’s why x^k+1 is used
Nice work @Comrade Rock Astley really well put solution
i kinda lost you on this step. are you saying to cancel out the x^r . x^k even when the denominator has an extra x in it? like can you explain how you took it from here

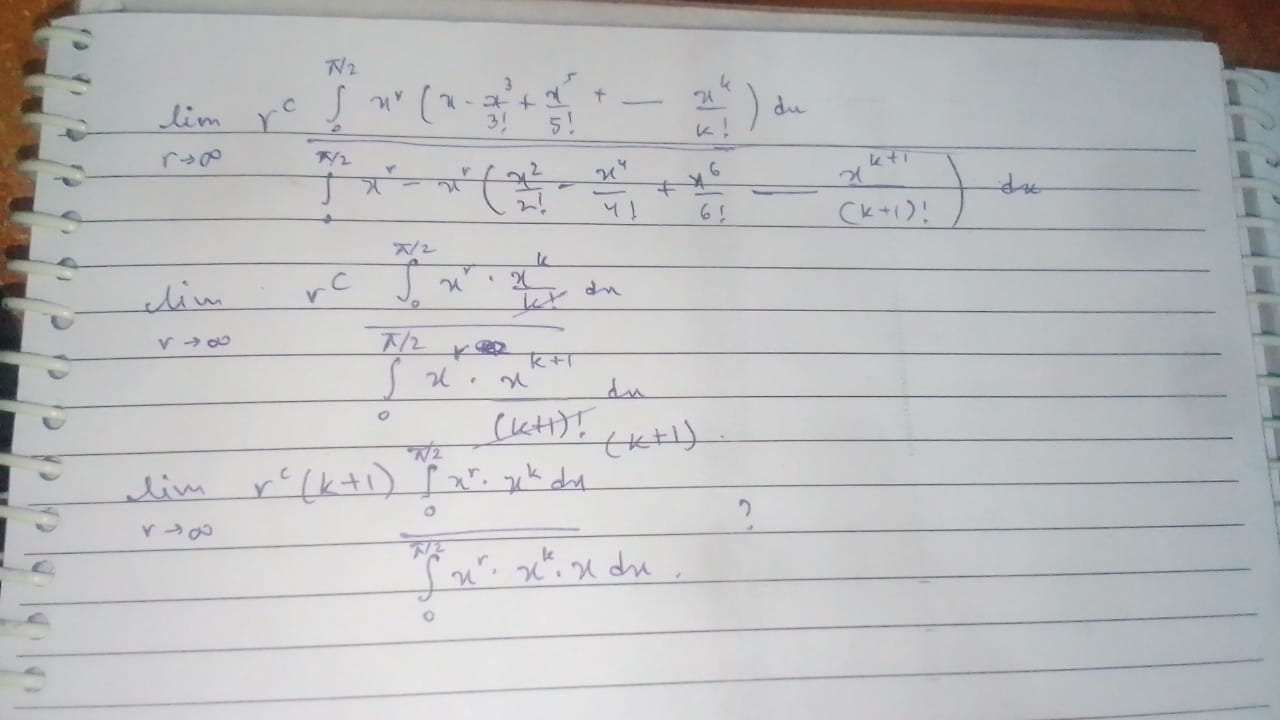
The denominators I’m talking about are the r+k+1 and r+k+2 you get after integrating
yeah go on just integrate normally from here
oh okayy. thankss so much, it was actually a very comprehensive solution
+solved @Comrade Rock Astley
Post locked and archived successfully!
Archived by
<@801817464425807892> (801817464425807892)
Time
<t:1714392765:R>
Solved by
<@769492044837552139> (769492044837552139)
