How even
a^2+b^2+c^2 = -2 aayega
Phir substitute a^2+b^2 = -c^2 and so on, uske aage kya karenge?
Given answer is 9
19 Replies
@Apu
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.What are the steps you did to get there?
a+b+c = 2, ab+bc+ca = 3, abc = 4 (roots relations)
(a+b+c)^2 =a ^2+b^2+c^2 +2(ab+bc+ca)
Put values, you get -2
The given cubic has 2 complex roots, so the sum CAN be -ve
nope look at the question: p/q -> p and q both are positive integers
That is the value of the expression given. The value of that can be anything.
There is no way of saying if that expression will be +ve or -ve just based on how it looks
Try this
It's long but...this is what I've got so far
so you get a^2 + b^2 + c^2 = -2
a^2 + b^2 = -2 -c^2
a^2+b^2 - c^2 = -2 - 2c^2
Similarly reduce the other denominators to -2-2a^2 and -2-2b^2
You now have
Comrade Rock Astley
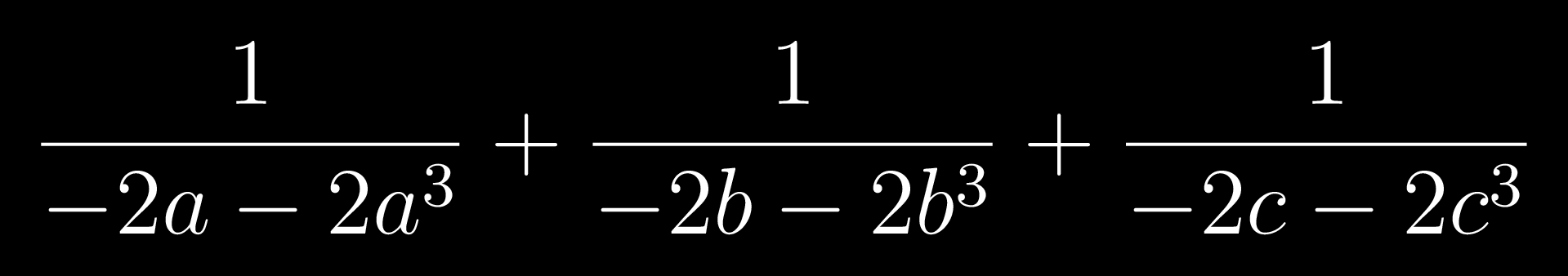
factor the -1/2 out
Now
Comrade Rock Astley
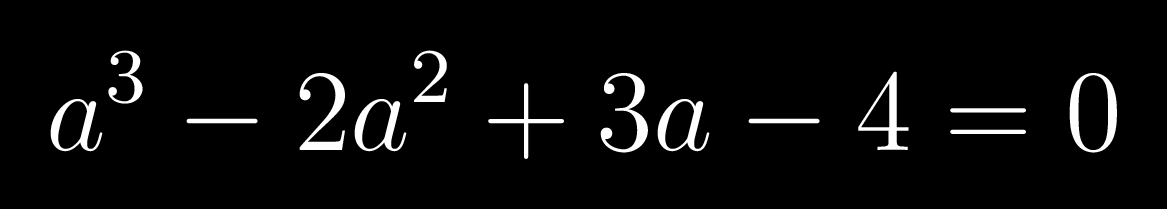
mera khudka ye glt tha paper mein
Comrade Rock Astley
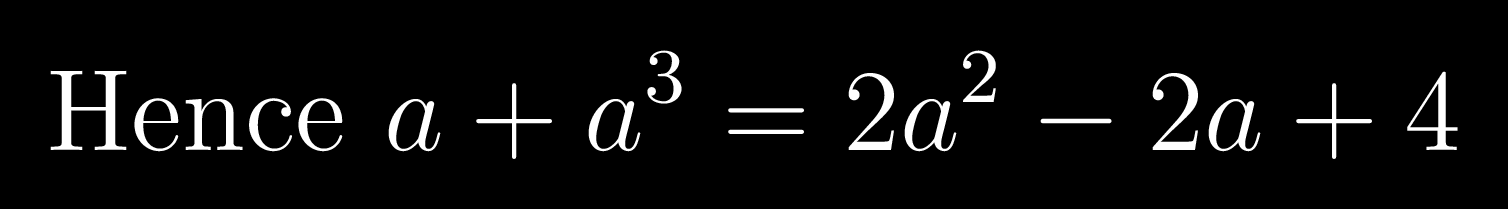
factor 2 out again
Comrade Rock Astley
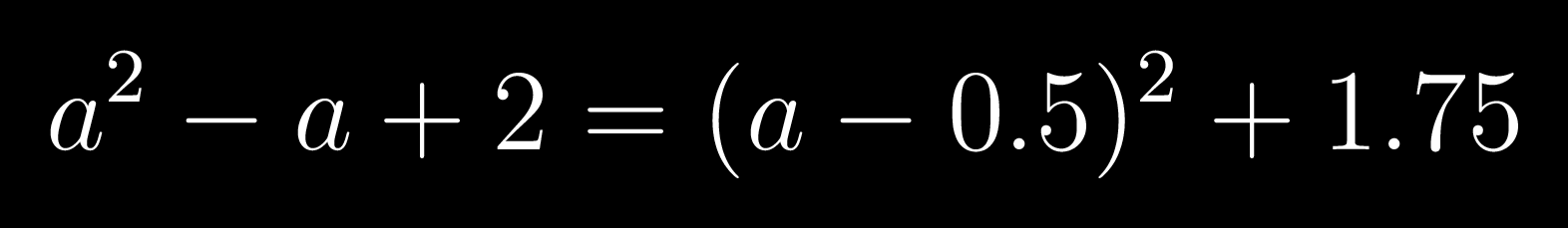
Similarly reduce the other denominators
Cross multiply and simplify
the denominator will come out to be very retarded, its gonna be hard to simplify that, koi pattern bhi nai mil raha
Can't use symmetricity of roots either since there are constant terms
yeah that denominator will be weird
(a(a-1)+2)(b(b-1)+2)(c(c-1)+2) = 2(a^2-a+b^2-b+c^2-c) + 8 + abc(a-1)(b-1)(c-1)
Oh well
Rewrite as a(a-1)+2 in the denominator after cross multiplying
It'll be easy then
did you get it?
saw the solution, they M&D'ed by(a-1) and in the denominator they got the cubic but differing by some constant, that led to the entire denominator getting simplified, after that it's trivial
+solved @Comrade Rock Astley
Post locked and archived successfully!
Archived by
<@318338770674122763> (318338770674122763)
Time
<t:1713711014:R>
Solved by
<@769492044837552139> (769492044837552139)