37 Replies
@Apu
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.,rotate

Rearrange the terms
You can write them as (31C1 - 31C2....) + 1/2 (31C2 +......) + 1/3 (31C3....)
and so on
Now we can reduce the series in each bracket into a usable term
We have:
Comrade Rock Astley
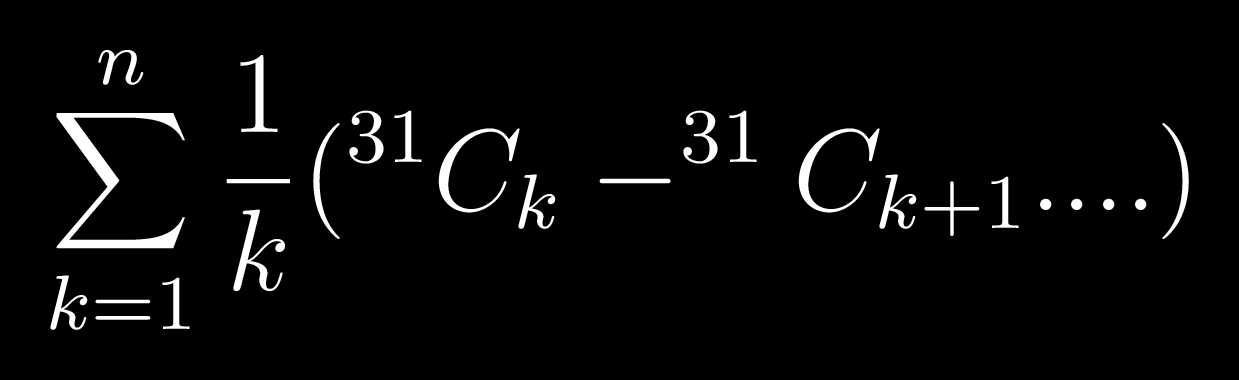
Now we'll simplify the series inside
Comrade Rock Astley
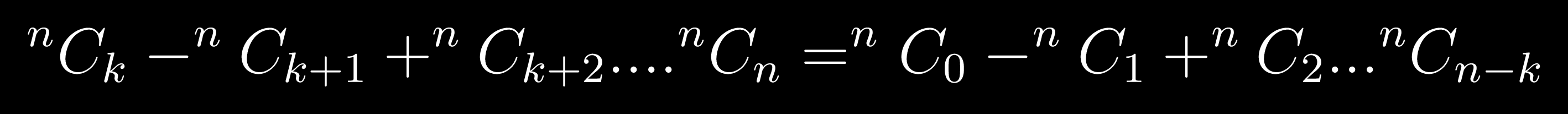
Actually it's
Comrade Rock Astley
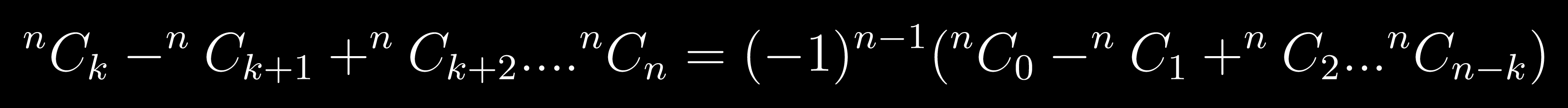
Can you simplify it?...mere se v nhi hua..
hold on
We'll get there
Ignore the -1 ^x part
We'll simplify the series inside this
So the best way to simplify this is to write this as a coefficient of x^k in some binomial expansion
Firstly we'll add x terms to it
Comrade Rock Astley
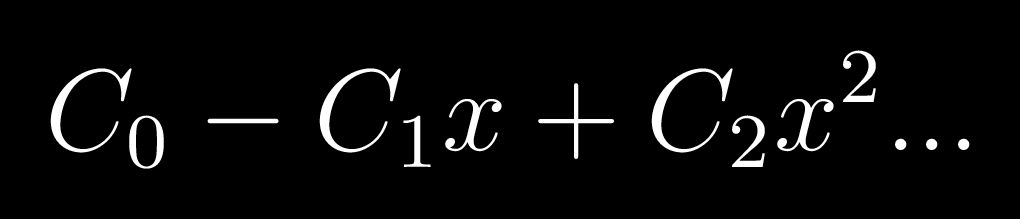
However this by itself cannot be used
We need to multiply this by something so that the exponent of x is constant in the result
Comrade Rock Astley
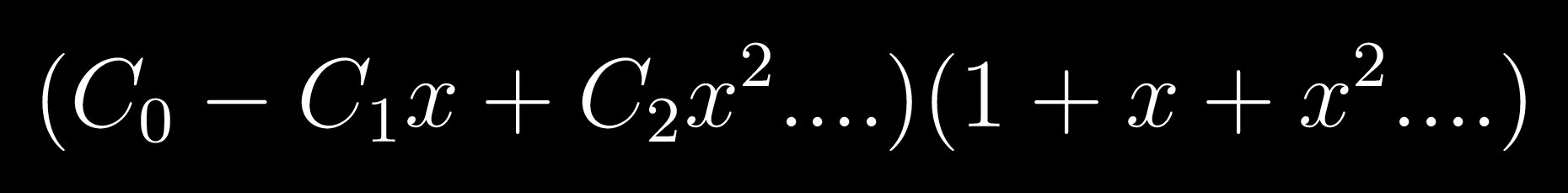
In this product we can find the coefficient of x^k
In the product we'll have this term
Comrade Rock Astley
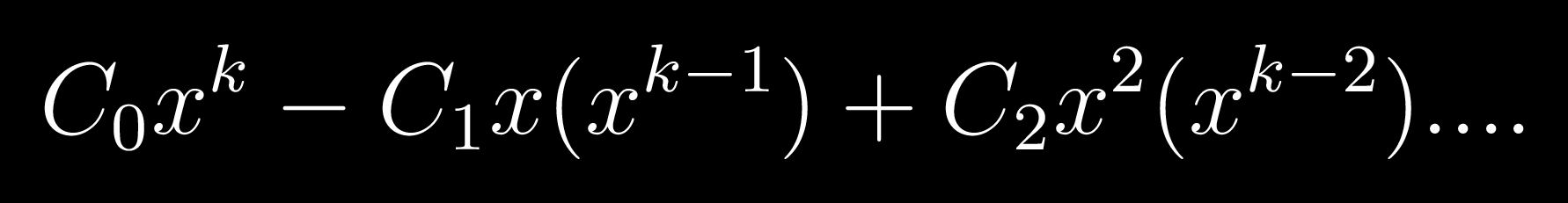
Hence we get:
Comrade Rock Astley
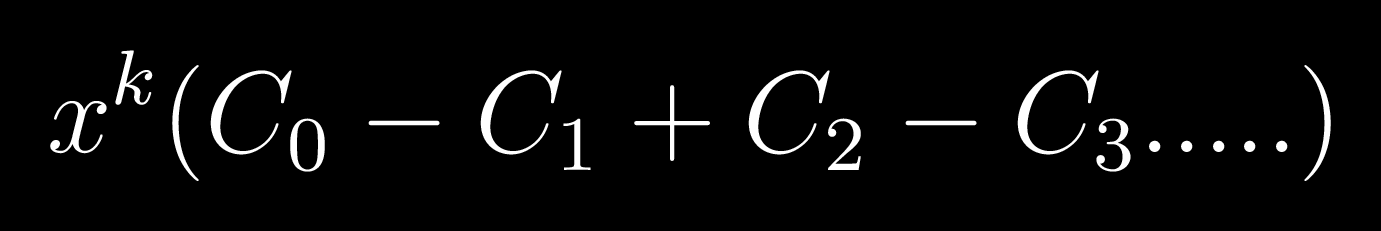
Please share written solution of yours...
Hence we see that the product of x^k in (C_0-C_1x+C_2x^2...(-1)^n C_nx^n) \times (1+x+x^2...) is what we need
...yeah
I'll put it in one doc
hold on
Okay

Woah lemme try...and what about 2nd question
Thank you
Did you find Q.no. 2 ka solution?
you know the rules of double sigma?
I think we have to make the series and again relate with coefficient of some expansion,im trying
Was out, just got back
Did you get anything so far?
Q2 looks symmetric at a glance
Try proving this:
Comrade Rock Astley
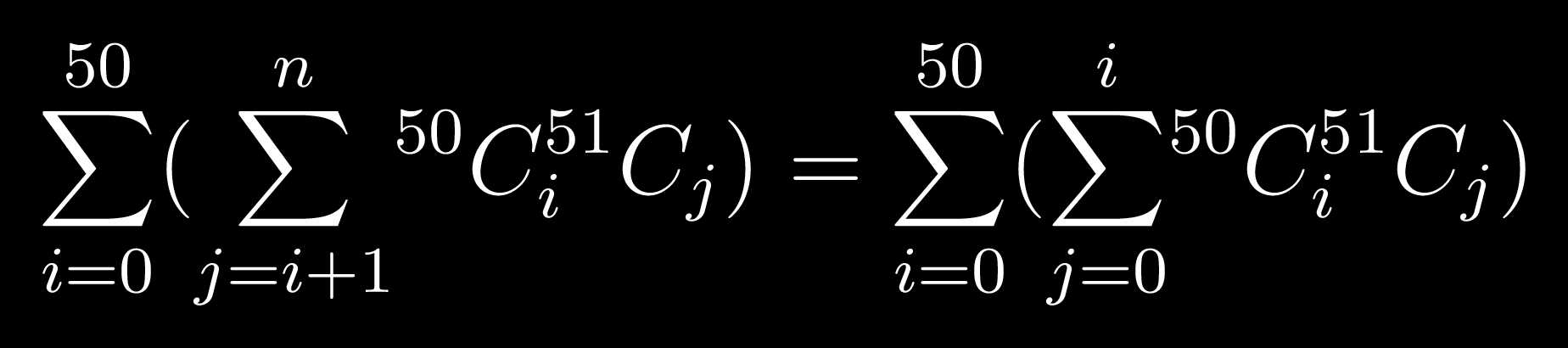
If you can prove this, then your answer is basically one step away
Just recognise what this means
and you'll easily get n
keeping i term constant
did you get it?
Yo @Ricky ?
all g
?
+solved @Comrade Rock Astley
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1714529521:R>
Solved by
<@769492044837552139> (769492044837552139)
