33 Replies
@Apu
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.where is this question
What do you have so far?
this question has a range but no defined value i think
thats it
i can think of the under root wala part but idk what do with the (-1)^n-1
sqrt (n^2+0.5 n+1) = n sqrt(1+1/2n+1/n^2) and you can approximate it to n as n goes to infinity
And since n is always a natural number sin (npi) is always 0
Should be 0 then
the answer? the answer is -1/root2
No not the answer
...I'll post after fully solving it one sec
@Comrade Rock Astleythis is the solution , can u just explain waht happened in the first 3 steps?
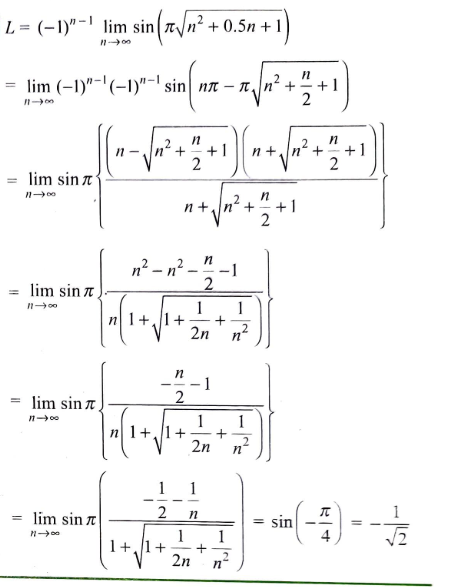
first 2 , third toh is just rationalization
There is one way to make that work
sin(x-n pi) or sin (x+ n pi) can be written as (-1)^n sin (x)
But then multiplying two oscillatory limits like that just looks wrong
trigo equations?
It's just sin(x-pi) = -(sinx)
and sin(x-2pi) = sinx
if you generalise that for natural numbers then sin (x- odd number times pi) = -sinx
and sin(x - even number times pi) = sinx
which is formally written as (-1)^n
ahh ok got it
I'm just very very skeptical about the second step
yea same thats what bugged me out too
I'll check if there's a way to solve without approximating like that
It might change the value
yes thats why i didnt wanna show the solution initially to get some different sort of approach from other people
Because if you include the 1/2n term but not the 1/n^2 term, you get exactly -1/ sqrt 2
neglecting the 1/2n and 1/n^2 in the denominator also gives -sinpi/4 tho?
Comrade Rock Astley
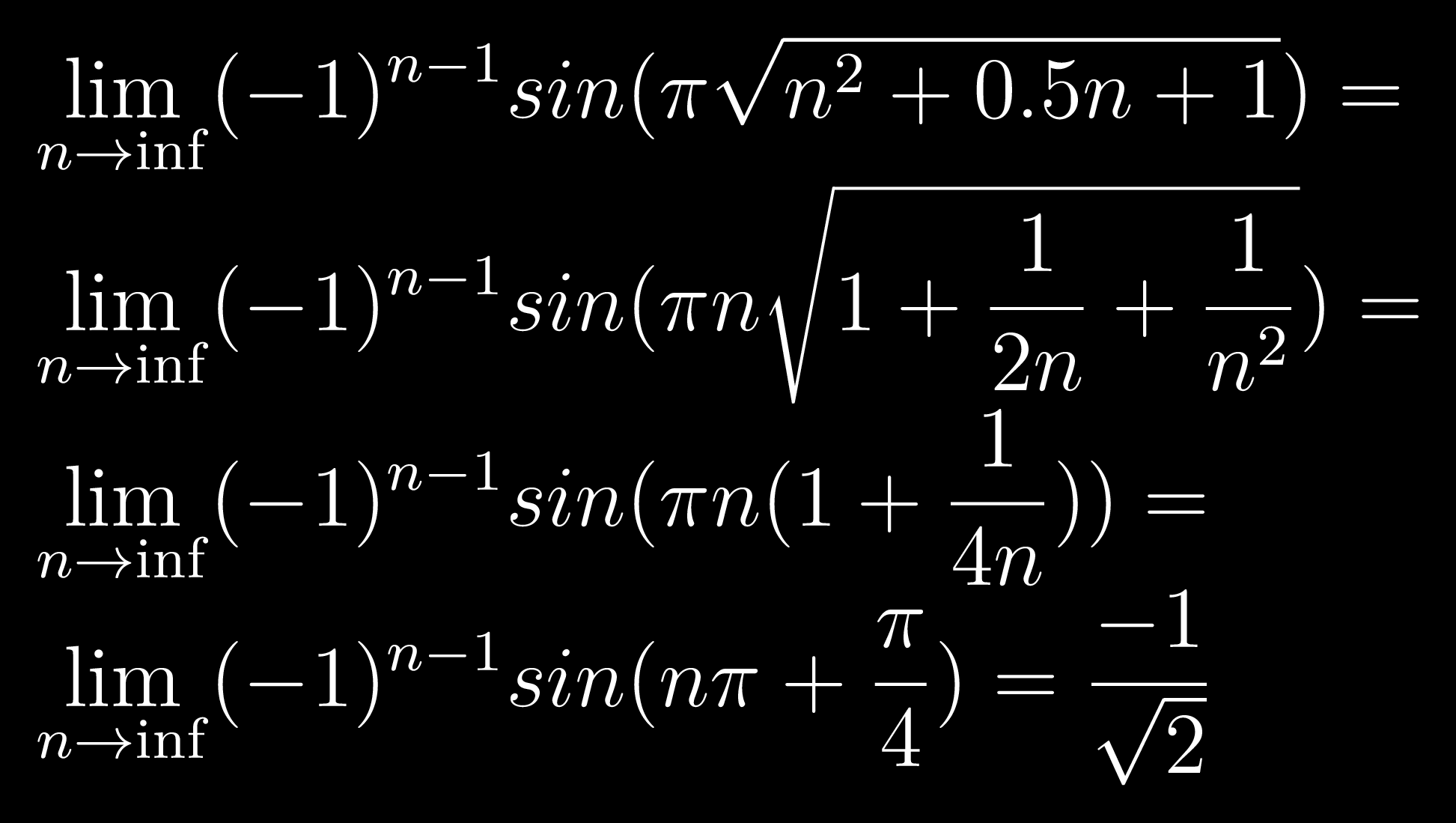
Well in the second step I neglected every term except 1 previously
which gives sin (n pi) times (-1)^n-1 which is 0 for natural numbers
Did you try a different approach?
i couldnt think of any
How did you get -sin pi/4 then?
no i said , looking at the solution i sent , in the last step if we neglect all the "n" wale terms , then we get -sinpi/4
Yeah in the given solution you can cancel them because you're not multiplying by n later
how did u get pi/4 in the last step here?
but then they've multiplied an oscillating limit with another oscillating limit, I don't know how well that works
If n is even you get -1 times 1/sqrt 2, if n is odd you get 1 times -1/sqrt 2
no i mean it was (1 + 1/4n) , putting the limit at n to infinity , 1/4n should tend to zero right?
You're also multiplying by n right after
Which tends to infinity
oh ok got it , this makes much more sense
+solved @Comrade Rock Astley
Post locked and archived successfully!
Archived by
<@862367568186310706> (862367568186310706)
Time
<t:1713461244:R>
Solved by
<@769492044837552139> (769492044837552139)
