28 Replies
@Gyro Gearloose
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.I tried solving and brainstomring on this but nothing worked , give me some hints or steps of approach i'll try on my own
You can equate magnitude of electric field by a point charge and magnitude of electric field given for a point like (R,0)
Solution 👇

If you have an answer then tell me if im correct or not
but this EF isn't due to the sphere.
Its due to charge
yea this is right
Do You understood the solution?
The motive behind this problem is to think about electric field due to infinite line charge.
Electric field can be written as alpha/r (r^) ( polar coordinate)
on comparing it with electric field due to infinite line charge you will get lambda=2(pi)(epsilon)(alpha)
Now consider an infinite line charge lying along z axis and it cuts the sphere than the length of that line inside sphere will be 2R so Q=lambda(2R) =4(pi)(epsilon)R(alpha)
I did the exact same thing for a plane and you did by assuming 3D
you cannot consider the electric field due to a point charge as for that the field should be given by E= alpha (x i + y j) / (x^2+y^2)^3/2
because it reduces to alpha (x i + y j)/root(x^2+y^2) * (1/x^2+y^2)
that is alpha/r^2 (r^) similar to electric field due to point charge
Can you write it on paper i can't understand the text form 😅
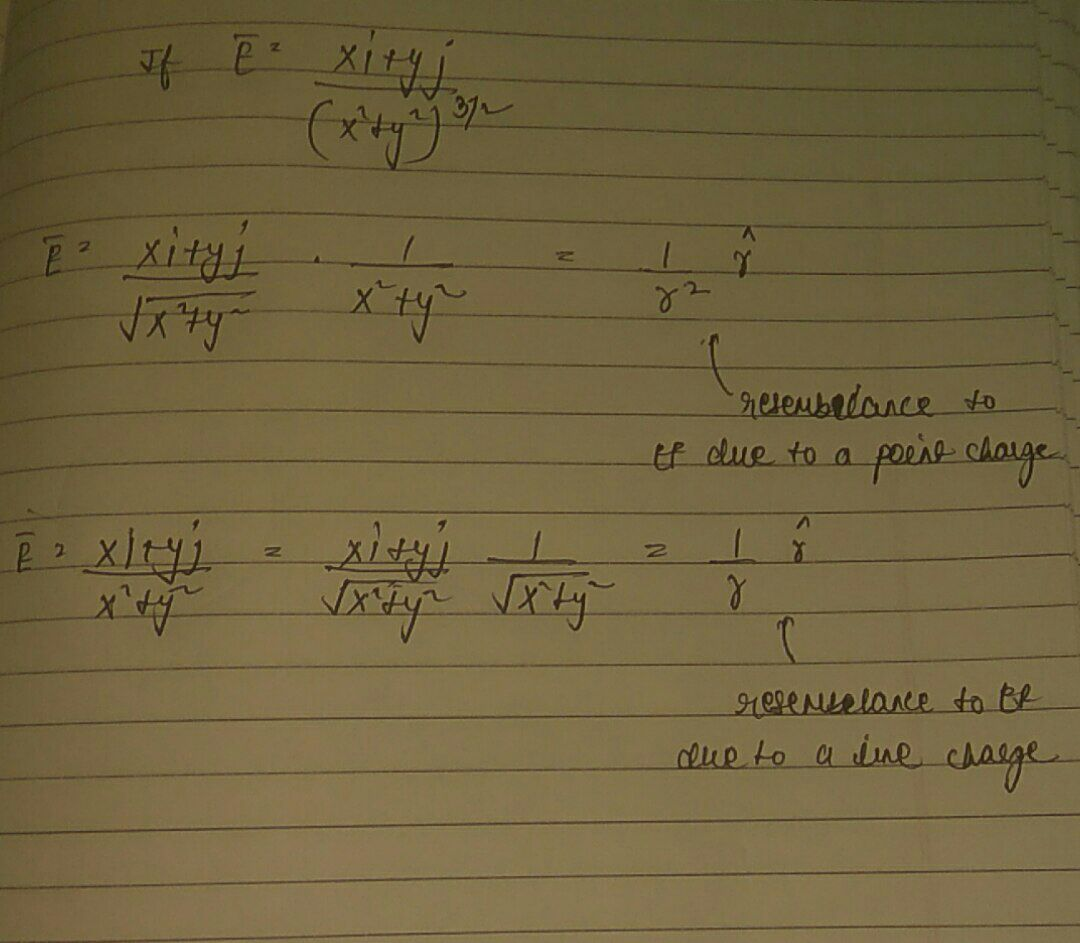
Ok ok then what is the flaw in my solution
You said that you assumed a charged particle placed at (0,0,0) and you equated the electric field due to that charged particle and the given electric field. From there you get the charge of the particle that you assumed to be placed at (0,0,0).Now as you are saying that the charge you calculated is equal to the charge of sphere basically you said that the charge placed at (0,0,0) is the charge that the sphere possess.So ultimately you are saying that the given electric field in question was of sphere and we need to calculate the charge possessed by it. And from there using shell theorem you assumed all charge at center and equated the electric field due to it and the given electric field .Now my question is, is it necessary that the given electric field is caused by the sphere only ? can't there be any external electric field existing in space in the given situation.
Like in my solution you can see i assumed the field produced due to infinite line charge kept along some axis (say z) and the portion of the line inside the sphere was the charge possessed.
Ohk I got it. I misunderstood the language and thought that both charge and circle have centre at origin. Thanks for correctting me.
I came up with another solution by using gauss's law and Concept of flux un non uniform electric field...

@Bhaumik_ @AS594
W, thank you both @AS594 @Priyam Alok
It would have been better if you assumed an arbitrary point in space and for that area vector direction would be along r^ and field direction would also have been along r^ and then writing gauss law.
Basically you fixed the y coordinate as per your first line so idk, like if there is an integration involving two variable and you assumed y=0 and then integrating it ,i don't find it correct as while integrating you should chose an arbitrary point rather than some point (say R,0).
Bro i couldn't take any arbitrary point for area vector in SPACE i could only take the points on the SPHERE. Thats how gauss's law works and putting any point on sphere then always x²+y² = R² and dot product of the area vector an Electric field will always be R as [(xî + yĵ).(xî + yĵ)]÷[(x²+y²)(x²+y²)^½] = R²^½ = R
I think i am absolutely correct in my position
From arbitrary point in space i meant an arbitrary point on the sphere (not (R,0)).
but no point of discussion "if you are absolutely correct" .
Bro i also mentioned the arbitrary condition which you are saying is also true. I only said that taking (R,0) is not wrong as it satisfies the eqution of sphere and pls be nice not sarcastic and chill bro galti sabse ho sakti hai mere se bhi hui thi na phli baar me
@Bhaumik_ i think your doubt is solved
yep thanks guys
+solved @Priyam Alok
Post locked and archived successfully!
Archived by
<@862367568186310706> (862367568186310706)
Time
<t:1713456221:R>
Solved by
<@582564114631491605> (582564114631491605)
