rolling motion
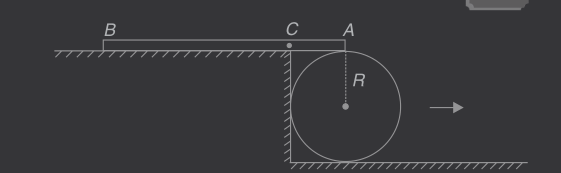
qs - AB is a non uniform plank of length L = 4R with
its centre of mass at C such that AC = R. It is
placed on a step with its one end A supported by a
cylinder of radius R as shown in figure. The centre
of mass of the plank is just outside the edge of the
step. The cylinder is slowly rolled on the lower
step such that there is no slipping at any of its
contacts. Calculate the distance through which
the centre of the cylinder moves before the plank
loses contact with the horizontal surface of the
upper step.
my ans - 3R/2
actual ans - R
10 Replies
@Gyro Gearloose
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.mera bhi 3/2 R aa rha hai
center x travel karega toh point A 2x travel karega wahi na?
2x = 3R
61 ans -
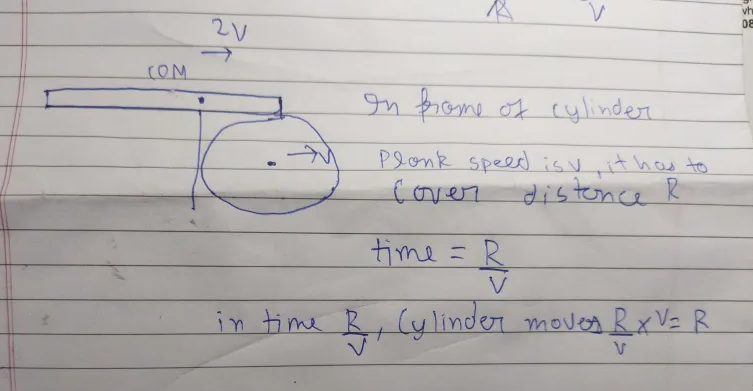
@Keshav Ohh wait i got it, When the COM of plank with reach the top of cylinder it will tend to move downwars, so the plank will get lifted from left and it will loose contact from the surface
so the center of mass of plank will have a displacement R right
How will we calculate displacement for the center of mass of cylinder??
@Keshav
+solved @Law of Reversibility
Post locked and archived successfully!
Archived by
<@1082354613749035099> (1082354613749035099)
Time
<t:1713145769:R>
Solved by
<@857920029584785428> (857920029584785428)